
Factor Analysis in R: Measuring Consumer Involvement

Peter Prevos |
1609 words | 8 minutes
Share this content
The first step for anyone who wants to promote or sell something is to understand the psychology of potential customers. Getting into consumers' minds is often problematic because measuring psychological traits is complex. Consumer involvement is a measure of people's attitudes towards a product or service. This article introduces the concept of consumer involvement. An example using data from tap water consumers illustrates the theory. This article analyses data collected from these consumers using factor analysis in R, with the psych package.
The most common method to measure psychological traits is to ask people several questions. Analysing this data is complicated because it is difficult to determine how the survey responses relate to the software of the mind. While the answers given by survey respondents are the directly measured variables, we like to know the hidden (latent) states in their minds. Factor Analysis is a technique that identifies latent variables within a data set, such as a customer survey.
The basic principle of measuring consumer attitudes is that their state of mind causes them to respond in a certain way. Factor analysis reverses this causality by analysing patterns in responses that indicate the consumer's state of mind. Using a computing analogy, factor analysis is a technique for reverse-engineering source code by analysing the input and output.
The data and code for this article are available on GitHub in the case-studies folder:
What is Consumer Involvement?
Involvement is a marketing metric that describes the relevance of a product or service in somebody's life. Judy Zaichkowsky defines consumer involvement formally as “a person's perceived relevance of the object based on inherent needs, values, and interests”. People who own a car will most likely be highly involved with purchasing and driving the vehicle due to the money involved and the social role it plays in developing their public self. Consumers will most likely have a much lower level of involvement with the instant coffee they drink than with their clothes.
Managerial Relevance
The level of consumer involvement depends on a complex array of factors. These factors relate to psychology, situational factors, and the service provider's marketing mix. The lowest level of involvement is considered a state of inertia which occurs when people habitually purchase a product without comparing alternatives.
From a managerial point of view, involvement is crucial because it is causally related to willingness to pay and perceptions of quality. Consumers with a higher level of involvement are willing to pay more for a service and have a more favourable perception of quality. Understanding involvement in the context of urban water supply is also crucial because sustainably managing water as a common pool resource requires the active involvement of all users.
Cult products have the highest possible level of involvement as customers are fully devoted to a particular product or brand. Commercial organisations use this knowledge to their advantage by maximising consumer involvement through branding and advertising. This strategy is used effectively by the bottled water industry. Manufacturers focus on enhancing the emotional aspects of their products rather than on improving the cognitive elements. Water utilities tend to use a reversed strategy and emphasise the cognitive aspects of tap water, the pipes, plants and pumps rather than trying to create an emotional relationship with their consumers.
Measuring Consumer Involvement
For my dissertation about customer service in water utilities, I measured the level of involvement that consumers have with tap water using the Personal Involvement Index (PII).

Customer Experience Management for Water Utilities: Marketing Urban Water Supply
Practical framework for water utilities to become more focused on their customers following Service-Dominant Logic.
Asking consumers directly about their level of involvement would not yield a stable answer, as each respondent would interpret the question differently. The best way to measure psychological states or psychometrics is to ask a series of questions linguistically related to the topic of interest.
The most cited method for measuring consumer involvement is the Personal Involvement Index, developed by Judy Zaichowsky. This index is a two-dimensional scale consisting of the following:
- Cognitive involvement (importance, relevance, meaning, value, and need)
- Affective involvement (involvement, fascination, appeal, excitement, and interest).
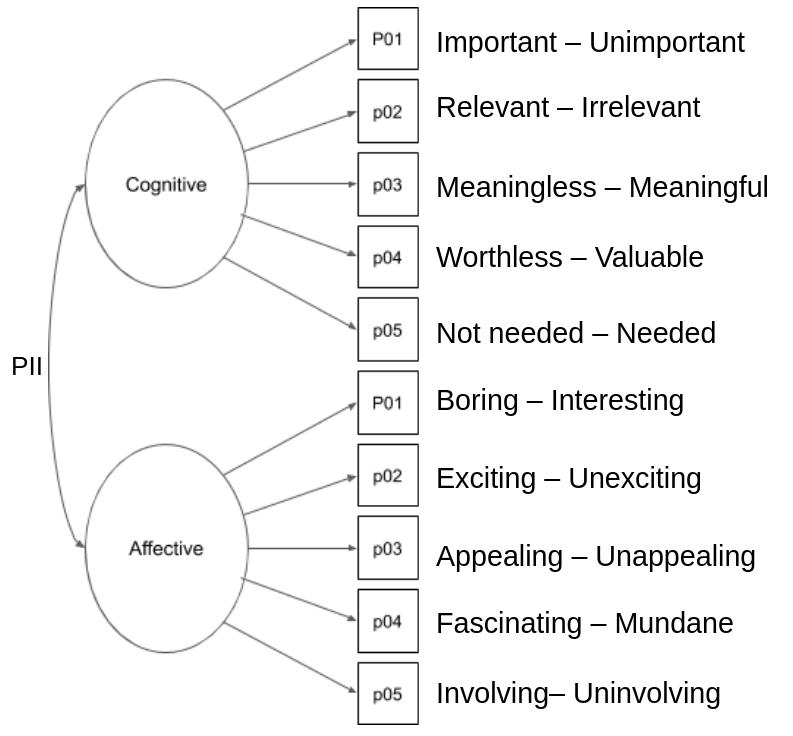
The survey instrument consists of ten Semantic Differential items. A Semantic Differential is a rating scale designed to measure the meaning of objects, events, or concepts. The researcher translates the concept, such as involvement, into a list of synonyms and their associated antonyms.
In the involvement survey, participants position their views along a continuum, such as Worthless-Valuable or Boring-Interesting. The level of involvement is the sum of all answers, ranging from 10 to 70.
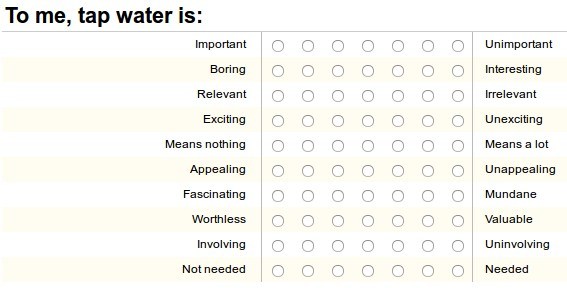
Obtaining the Data
The data form part of a survey of tap water customers.
## Consumer Involvement
library(tidyverse)
library(psych)
# Clean data
customers <- read_csv("data/customer_survey.csv")[-1, ] %>%
type_convert() %>%
filter(is.na(term)) %>%
select(c(1, 21:51, -33)) %>%
rename(customer_id = 1)The scale uses reverse polarity as some of the items are from low to high (boring – interesting) and others from high to low (important – unimportant), so we need to correct this by reversing the scores for six items. The data also has missing values, so we only use the complete cases.
# Correct polarity
pii <- select(customers, customer_id, starts_with("p")) %>%
mutate(p01 = 8 - p01,
p02 = 8 - p02,
p07 = 8 - p07,
p08 = 8 - p08,
p09 = 8 - p09,
p10 = 8 - p10)
# Remove missing values
pii <- pii[complete.cases(pii), ]Exploratory Analysis
This data set contains additional information, and the code selects only variable names that start with "p" (for the Personal Involvement Inventory). Before we analyse data, we remove customers who provided the same answers to all items or did not respond to all questions. These responses are most likely invalid, which leaves 757 rows of data.
A boxplot is a convenient way to visualise responses to multiple survey items in a single chart. This plot immediately shows an interesting pattern in the answers. Responses to the first five items were generally higher than those for the last five. This result indicates a distinction between cognitive and affective involvement.
# Visualise PII
pii_long <- pii %>%
pivot_longer(-customer_id, names_to = "Item", values_to = "Response")
ggplot(pii_long) +
aes(Item, Response) +
geom_boxplot(fill = "#f7941d") +
theme_bw(base_size = 12) +
labs(title = "Personal Involvement Index",
subtitle = paste0("Tap Water Consumers USA and Australia (n = ",
nrow(pii), ")"))
The next step in the exploratory analysis is to investigate how these factors correlate. The correlation plot below shows that all items strongly correlate with each other. As shown in the boxplots above, the first five and the last five items correlate more strongly. This plot suggests that the two dimensions of the involvement index correlate. The following section shows how to use factor analysis in R to check the significance of these correlation patterns.
# Visualise correlation matrix
c_matrix <- cor(pii[, -1])
library(ggcorrplot)
ggcorrplot(c_matrix, outline.col = "white") +
labs(title = "Personal Inventory Index",
subtitle = "Correlation Matrix")
Factor Analysis in R
Researchers often confuse Factor Analysis with Principal Component Analysis. The outcomes are very similar when applied to the same data set. Both methods are similar but serve different purposes. Principal Component Analysis is a data-reduction technique that reduces the number of variables in a problem. The specific purpose of Factor Analysis is to uncover latent variables. The mathematical principles for both methods are similar but not identical, and they should not be confused.
One of the most crucial decisions in factor analysis is to decide how to rotate the factors. There are two types: orthogonal and oblique. In simple terms, orthogonal rotations reduce the correlation between dimensions, whereas oblique rotations allow dimensions to relate to each other. Because of the strong correlations in the correlation plot and the fact that both dimensions measure involvement, this analysis uses oblique rotation. The visualisation below shows how each item and the two dimensions relate to one another.
library(psych)
pii_fa <- fa(pii[, -1], nfactors = 2, rotate = "oblimin", fm = "ml")
fa.diagram(pii_fa, main = NULL, marg = c(0, 8, 0, 0))
Consumer Involvement Scores
This analysis suggests that the items for the PII measure an underlying construct, which we can call consumer involvement. To work out the scores for this measure, we can sum the items for each respondent.
# Calculating the PII
pii_scores <- pii %>%
mutate(cognitive = p01 + p02 + p03 + p04 + p05,
affective = p06 + p07 + p08 + p09 + p10) %>%
select(customer_id, cognitive, affective) %>%
pivot_longer(cols = -customer_id)
ggplot(pii_scores) +
aes(value) +
geom_histogram(fill = "dodgerblue 4", binwidth = 1) +
facet_wrap(~name) +
theme_minimal(base_size = 12) +
labs(title = "Consumer Involvement with Tap Water",
subtitle = "Personal Involvement Index",
x = "Score", y = NULL)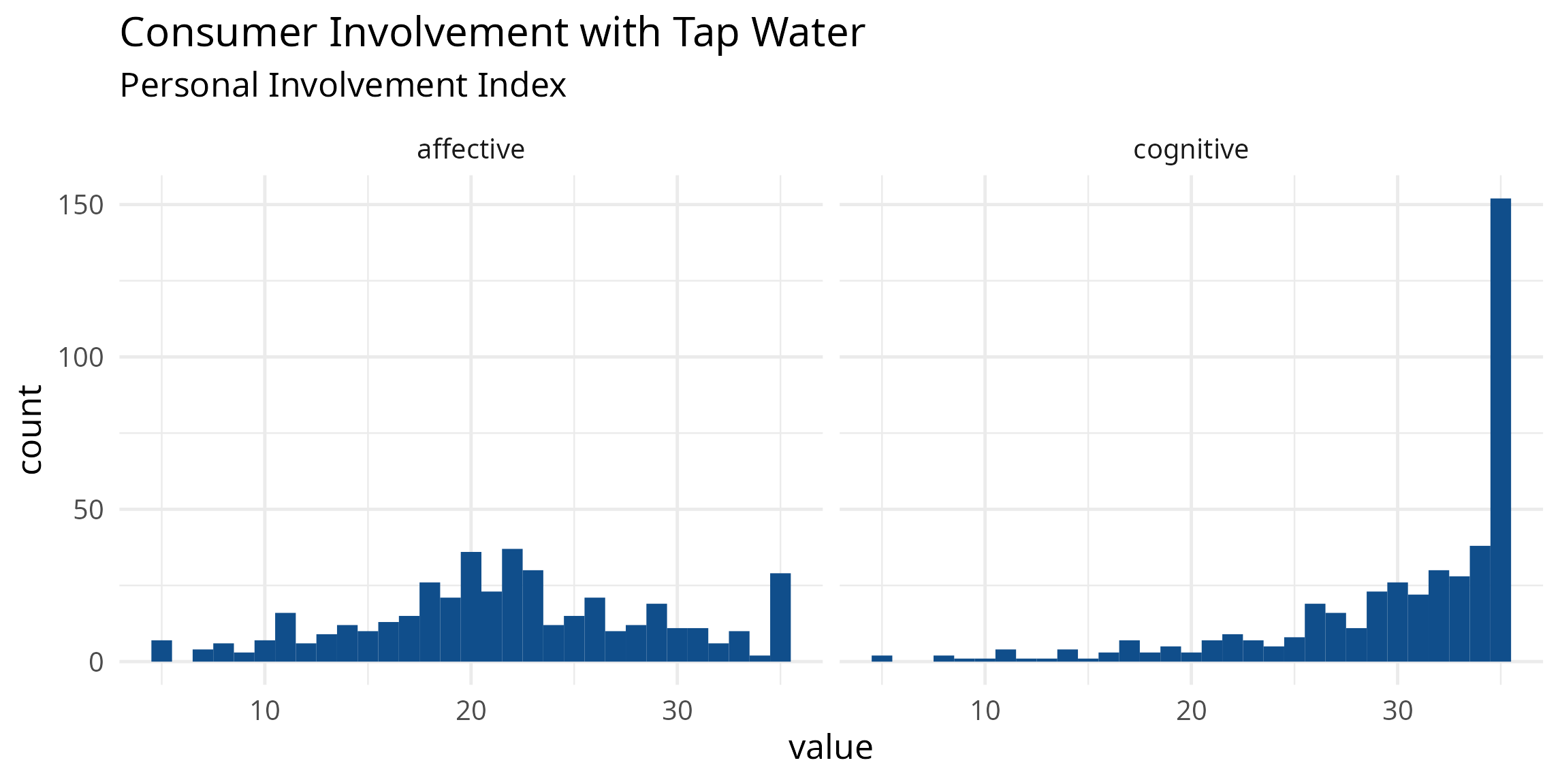
This simple factor analysis in R shows the basic principle of analysing psychometric data. The psych package has many more specialised tools to dig deeper into the information. This article has not assessed this construct's validity or evaluated the factors' reliability. That may be for a future article.
Chapter 8 in Data Science for Water Utilities explains the principles of analysing survey data to understand the customer experience in more detail.

Data Science for Water Utilities
Data Science for Water Utilities published by CRC Press is an applied, practical guide that shows water professionals how to use data science to solve urban water management problems using the R language for statistical computing.
Share this content


