Call Centre Workforce Planning Using Erlang C in R language

The Erlang C formula describes the probability that a customer needs to queue instead of being immediately serviced $(P_w)$. This formula is closely related to the Poisson distribution, which describes queues such as traffic lights or hospital waiting lists.

$$P_w = \frac{\frac{A^N}{N!}\frac{N}{N-A}}{\Big( \sum_{i=0}^{N-1} \frac{A^i}{i!} \Big)+\frac{A^N}{N!}\frac{N}{N-A}}$$

The intensity of traffic $A$ is the number of calls per hour multiplied by the average duration of a call. Traffic intensity is measured in dimensionless Erlang units, which expresses the time it would take to manage all calls if they arrived sequentially. The intensity measures the effort that needs to be undertaken in an hour. In reality, calls arrive at random times during the hour, which is where the Poisson distribution comes in. The waiting time is also influenced by the number of available operators $N$.

Both common sense and the formula show that increasing the number of calls or decreasing the number of operators increases the likelihood that customers are placed in a queue. The more staff, the higher the service level, but how many people do you need to achieve your desired grade of service efficiently?

The Grade of Service $S$ is a function of the outcome of the Erlang C formula ($P_w$), the number of agents ($N$), the call intensity ($A$), call duration ($\lambda$) and lastly the target answering time ($t$).

The Erlang C formula can be reworked to provide that answer. I sourced this solution from callcenterhelper.com. We now have a toolset for call centre planning which we can implement in the R language.

$$S = 1 - \Large[ P_w e^ {-[(N-A](t/ \lambda)]} \large]$$

The Erlang C formula contains some factorials and powers, which become problematic when dealing with significant call volumes or many agents. The Multiple Precision Arithmetic library enables working with large integer factorials, but there is no need to wield such strong computing powers. To make life easier, the Erlang C formula includes the Erlang B formula, the inverse of which can be calculated using a small loop.

This implementation is very similar to an unpublished R package by Patrick Hubers, enhanced with work from callcenterhelper.com. This code contains four functions:

1. intensity: Determines intensity in Erlangs based on the rate of calls per interval, the total call handling time and the interval time in minutes. All functions default to an interval time of sixty minutes. Erlangs are a dimensionless unit as a measure of the offered load.
2. erlang_c: Processes the Erlang C formula using the number of agents and the variables determining intensity (call rate and call handling time). The output is the probability that a customer has to wait for service.
3. service_level: Calculates the service level. The inputs are the same as above, plus the period for the Grade of Service in seconds.
4. resource: Seeks the number of agents needed to meet a Grade of Service. This function starts with the minimum number of agents (the intensity plus one agent) and keeps searching until it finds the number of agents that achieve the desired Grade of Service.

  ## Call Centre Workforce Planning Using Erlang C in R language
  
  ## Erlang-C Functions
  intensity <- function(rate, duration, interval = 60) {
      (rate / interval) * duration
  }

  erlang_c <- function(agents, rate, duration, interval = 60) {
      int <- intensity(rate, duration, interval)
      erlang_b_inv <- 1
      for (i in 1:agents) {
          erlang_b_inv <- 1 + erlang_b_inv * i / int
      }
      erlang_b <- 1 / erlang_b_inv
      agents * erlang_b / (agents - int * (1 - erlang_b))
  }

  service_level <- function(agents, rate, duration, target, interval = 60) {
      pw <- erlang_c(agents, rate, duration, interval)
      int <- intensity(rate, duration, interval)
      1 - (pw * exp(-(agents - int) * (target / duration)))
  }

  resource <- function(rate, duration, target, gos_target, interval = 60) {
      agents <- round(intensity(rate, duration, interval) + 1)
      gos <- service_level(agents, rate, duration, target, interval)
      while (gos < gos_target * (gos_target > 1) / 100) {
          agents <- agents + 1
          gos <- service_level(agents, rate, duration, target, interval)
      }
      return(c(agents, gos))
  }

For example, you manage a call centre with 100 calls every 30 minutes and an average handling time of 3 minutes. These numbers result in an intensity of intensity(100, 3, 30) 10 Erlangs or ten calls hours of traffic per hour. This result means we need at least ten agents, assuming all calls arrive neatly after each other.

The reality of a contact centre is chaotic, as calls arrive randomly, so there is a high probability that an operator will be busy if we only use ten agents. You can enter this data into the Erlang C in R function to find the chance a customer needs to wait. With ten agents, the likelihood is 100%. With 11 agents, it is 68%. The sapply function helps to view the impact of adding more customer service agents.

  erlang_c(11, 100, 3, 30)
  [1] 0.6821182

  sapply(10:20, erlang_c, rate = 100, duration = 3, interval = 30)
  [1] 1.000000000 0.682118205 0.449388224 0.285270453 0.174131934 0.102042367
  [7] 0.057340331 0.030876110 0.015928277 0.007873558 0.003731126

The likelihood of a customer having to wait is the main target for any service that involves queueing. We need to set a target service level or Grade of Service. The service_level function calculates the Grade of Service using the previous parameters plus the target in seconds. Let's make some assumptions:

• Required Grade of Service 80%
• Target answer time: 20 seconds

Using the function, we can quickly see that with 11 agents and 100 calls per 30 minutes, we only have a Grade of Service of 39%, much less than the required 80%. Using sapply(), we can see that we need just over 13 available agents.

The resource() function ties everything together and seeks the number of agents needed to meet the required grade of service. We need at least 14 available agents to answer 80% of calls within 20 seconds, which gives us an actual predicted Grade of Service of 88%.

  ## Example
  service_level(agents = 11, rate = 100, duration = 3, target = 20 / 60, interval = 30)

  service <- data.frame(agents = 10:20,
                        GoS = sapply(10:20, service_level, rate = 100, duration = 3, target = 20 / 60, interval = 30))

  library(ggplot2)
  ggplot(service, aes(agents, GoS)) +
    geom_line() +
    scale_x_continuous(breaks = 10:20) + 
    scale_y_continuous(labels = scales::percent) +
    geom_hline(yintercept = 0.8, col = "blue") +
    theme_bw(base_size = 10) + 
    labs(title = "Call Centre Simulation",
         subtitle = "Erlang-C Formula")
  ggsave("call-centre-example.png", width = 6, height = 4)

  resource(rate = 100, duration = 3, target = 20/60, gos_target = 80, interval= 30)

I used the Erlang C model to recommend staffing levels in a contact centre some years ago. This experience taught me that the mathematical model is the first step towards call centre workforce planning. Several other metrics can be built on the Erlang C model, such as agents' average occupancy and handling time.

Like all mathematical models, the Erlang C formula is an idealised version of reality. Agents are not always available; they need breaks, toilet stops and might even go on leave. Employers call this loss of labour shrinkage, a somewhat negative term to describe something positive for the employee. The Erlang C model provides the number of 'bums on seats'.

Like every model, the Erlang C formula is not a perfect representation of reality. The formula tends to overestimate the required resources because it assumes that people will stay on hold indefinitely, while the queue will automatically shorten as people lose patience.

The number of employees needed to provide this capacity depends on the working conditions at the call centre. For example, if employees are only available to take calls 70% of their contracted time, you will need $1/0.7=1.4$ staff members for each live agent to meet the Grade of Service.

Another problem is the stochastic nature of call volumes and handling times. The Erlang C model requires a manager to estimate call volume and handling time (intensity) as a static variable, while in reality, it is stochastic and subject to variation. Time series analysis can help to predict call volumes, but every prediction has a degree of uncertainty. We can manage this uncertainty by using a Monte Carlo simulation.

All the functions listed above can be rewritten to provide a vector of possible answers based on the average call volume and duration and their standard deviation. This simulation assumes a normal distribution for both call volume and the length of each call. The outcome of this simulation is a distribution of service levels.

Monte Carlo Simulation

A Monte Carlo simulation is a method to simulate reality by defining a probability distribution of the events in the model.

For example, a call centre receives, on average, 100 calls per half hour with a standard deviation of 10 calls. The average time to manage a call, including wrap-up time after the call, is 180 seconds, with a standard deviation of 20 seconds. The centre needs to answer 80% of calls within 20 seconds. What is the likelihood of achieving this level of service?

The average intensity of this scenario is 10 Erlangs. Using the resource formula suggests that we need 14 agents to meet the Grade of Service. Simulating the intensity of the scenario 1000 times indicates that the intensity is between 5.4 and 15.9 Erlangs (see code at the end of this article).

  resource(100, 180, 20, 80, 30)
  [1] 14.0000000 0.88835

  intensity_mc(100, 10, 180, 20) %>% summary()
  
  Min. 1st Qu. Median Mean 3rd Qu. Max.
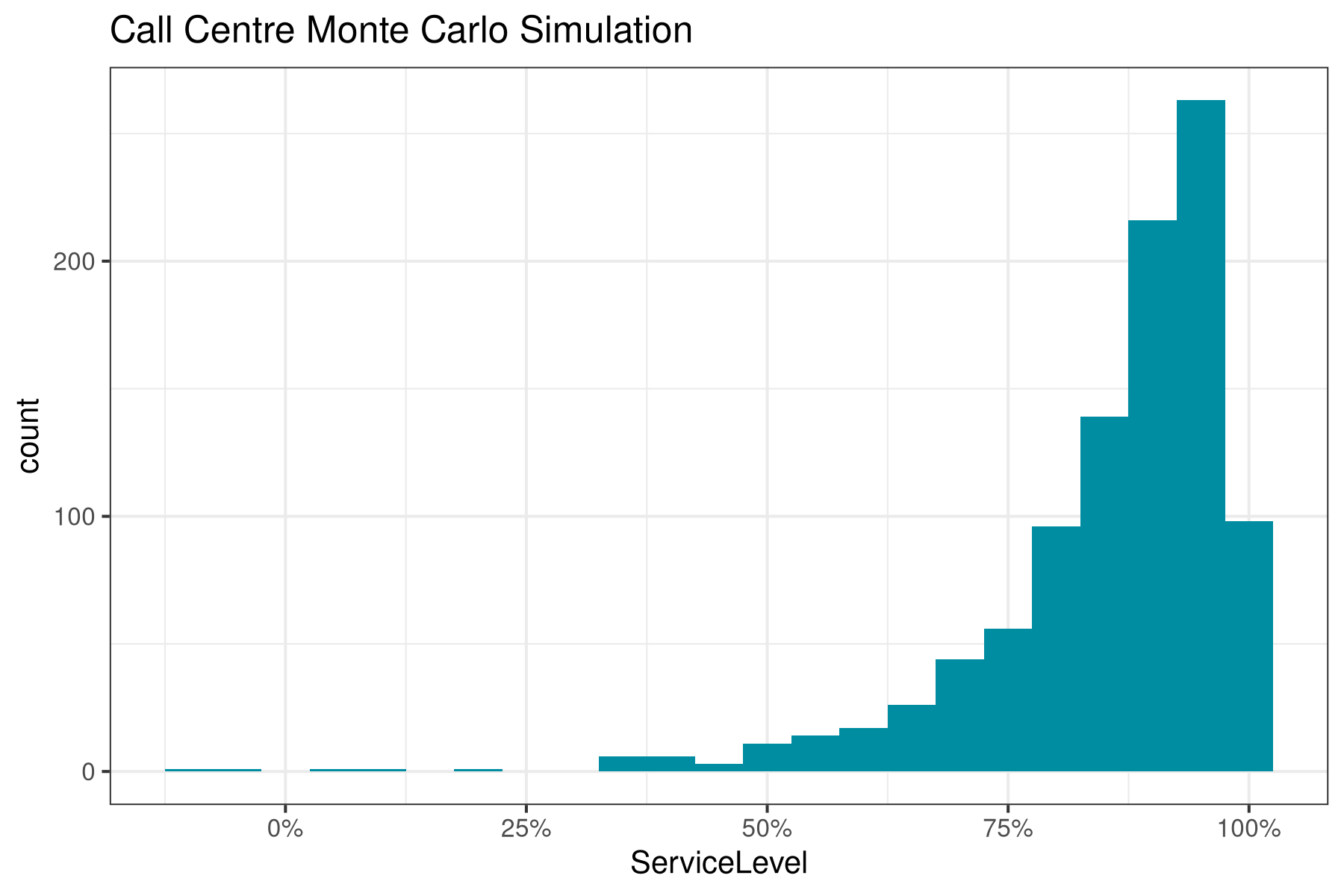
  5.480 8.975 9.939 10.025 10.993 15.932

The next step is to simulate the expected service level for this scenario. The plot visualises the outcome of the Monte Carlo simulation and shows that in 95% of situations, the Grade of Service is more than 77% and half the time, it is more than 94%.

  service_level_mc(15, 100, 10, 180, 20, 20, 30, sims = 1000) %>%
  + quantile(c(.05, .5, .95))
  5% 50% 95%
  0.7261052 0.9427592 0.9914338

This article shows that Erlang C in R helps managers plan call centre workforce. We may need a Shiny application to develop a tool to manage the complexity of these functions. I would love to hear from people with practical experience in managing call centres in how they analyse data.

  ## Monte Carlo Simulation
  
  library(tidyverse)

  intensity_mc <- function(rate_m, rate_sd, duration_m, duration_sd, interval = 60, sims = 1000) {
    (rnorm(sims, rate_m, rate_sd) / (60 * interval)) * rnorm(sims, duration_m, duration_sd)
  }

  intensity_mc(100, 10, 180, 20, interval = 30) %>%
    summary()

  erlang_c_mc <- function(agents, rate_m, rate_sd, duration_m, duration_sd, interval = 60) {
    int <- intensity_mc(rate_m, rate_sd, duration_m, duration_sd, interval)
    erlang_b_inv <- 1
    for (i in 1:agents) {
      erlang_b_inv <- 1 + erlang_b_inv * i / int
    }
    erlang_b <- 1 / erlang_b_inv
    agents * erlang_b / (agents - int * (1 - erlang_b))
  }

  service_level_mc <- function(agents, rate_m, rate_sd, duration_m, duration_sd, target, interval = 60, sims = 1000) {
    pw <- erlang_c_mc(agents, rate_m, rate_sd, duration_m, duration_sd, interval)
    int <- intensity_mc(rate_m, rate_sd, duration_m, duration_sd, interval, sims)
    1 - (pw * exp(-(agents - int) * (target / rnorm(sims, duration_m, duration_sd))))
  }

  tibble(ServiceLevel = service_level_mc(agents = 14,
                                         rate_m = 100,
                                         rate_sd = 10,
                                         duration_m = 180,
                                         duration_sd = 20,
                                         target = 20,
                                         interval = 30,
                                         sims = 1000)) %>%
    ggplot(aes(ServiceLevel)) +
    geom_histogram(binwidth = 0.05, fill = "#008da1") +
    scale_x_continuous(labels = scales::percent) + 
    theme_bw(base_size = 10) +
    labs(title = "Call Centre Monte Carlo Simulation")